
Initialization
In[403]:=

Usage
In[607]:=
![]()
Out[607]=
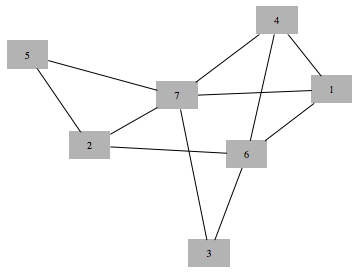
Make graph' s vertex list sorted
This is helpful when switching between labeled graph and adjacency matrix representation
![]()
Out[604]=
![]()
Out[606]=
![]()
Check if the graph is chordal
In[477]:=
![]()
Out[477]=
![]()
Find minimum fill triangulation
In[567]:=

Out[569]=
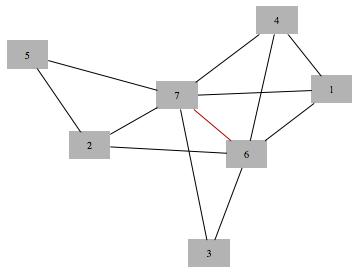
![]()
Get perfect elimination ordering, and rearrange graph vertices in elimination order
In[572]:=
![]()
Out[573]=
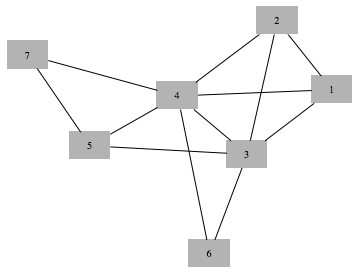
Check that vertices are now in perfect elimination order
In[574]:=
![]()
Out[574]=
![]()
Get 0 - fill Cholesky factorization of adjacency matrix in perfect elimination order
In[578]:=

Out[581]=
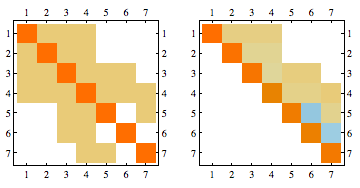
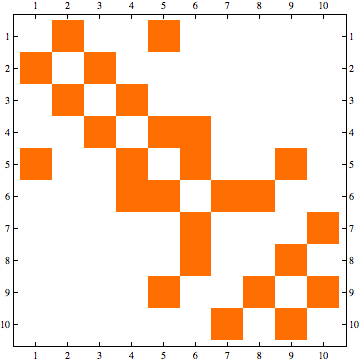
Arrange matrix in minimum fill order
In[641]:=
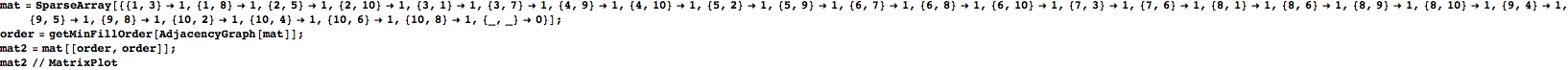
Out[644]=
Relabel graph vertices in minimum fill order
In[651]:=
![]()
Out[652]=
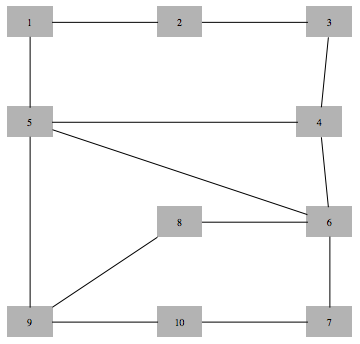
Out[653]=
![]()
Get min - fill Cholesky factorization of the matrix
In[675]:=
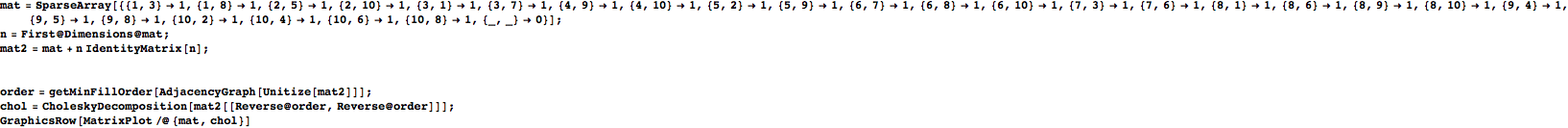
Out[680]=
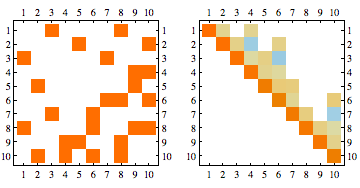
Get min - fill triangulation of the corresponding graph
In[697]:=
![]()
Out[699]=
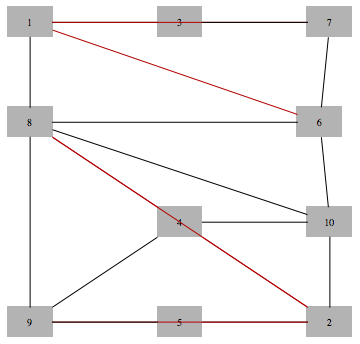
Get all maximal cliques of the chordal graph
In[703]:=
![]()
Out[704]=
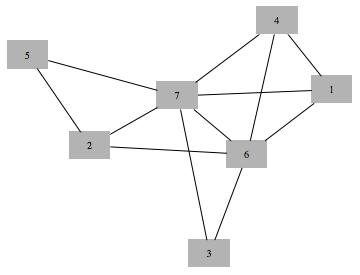
Out[705]=
![]()
Get maximal cliques of non-chordal graph
These are cliques that are found using maximum cardinality search
In[708]:=
![]()
Out[708]=
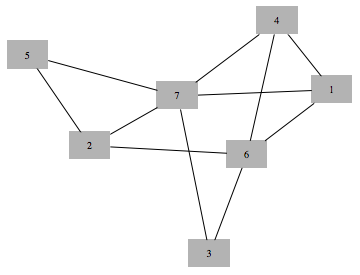
Out[709]=
![]()
Create chordal graph with given clique-tree structure and tree width
In[717]:=
![]()
Out[717]=
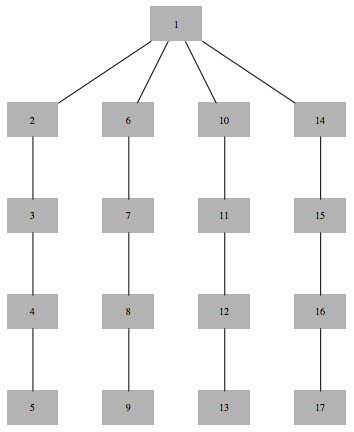
Out[718]=
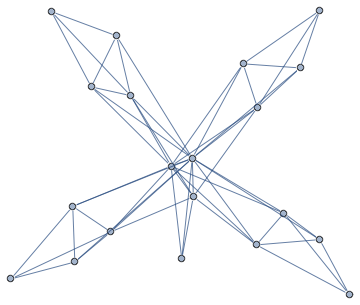
Recover original clique tree structure from a chordal graph
In[722]:=
![]()
Out[723]=
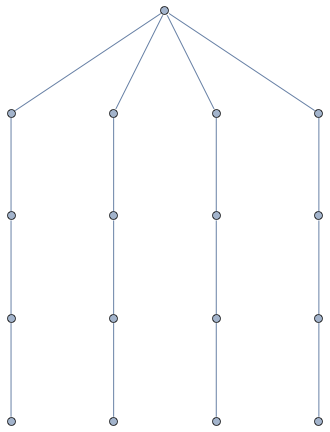
Out[724]=
![]()