Cavity method to count colorings
Sometimes we have an easy way to find marginal probabilities of spin configurations, cavity method gives us a way to combine those marginal probabilities to get a partition functon.
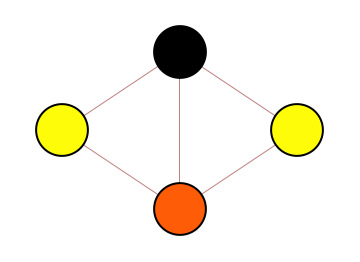
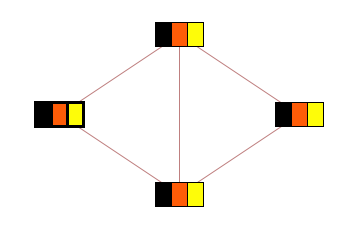
For example, consider all possible ways of coloring a kite graph
 |
 |
 |
 |
 |
 |
Taking all configurations to be equally likely, we can see from this that the probability of the leftmost node taking black color is 1/3. In the graph above, this can be found by counting all configurations, however more efficient methods exist to find this marginal probability. The question is now whether we can combine such probabilities to find the total number of configurations.
Step 0 : pick some arbitrary order over vertices

![]()
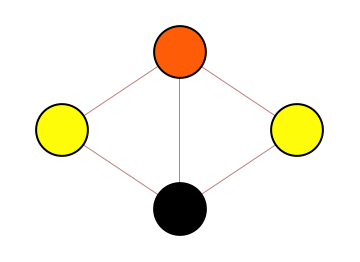
Step 1 : pick an arbitrary proper coloring using greedy method
Step 2 : suppose proper colorings are sampled uniformly, find the probability of first vertex assuming the color picked for it in Step 1
By symmetry, this value is 1/3
Step 3 : remove this vertex, and remove it's color from the list of allowed colors for adjacent vertices.

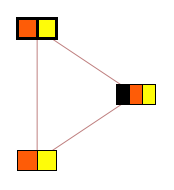
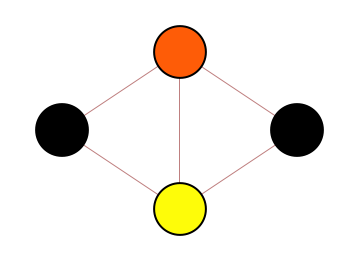
Step 4 : find probability of the next node taking it' s assigned color
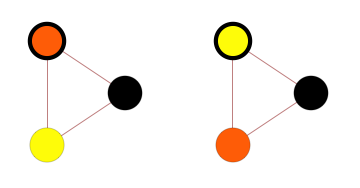
By symmetry you can see this value is 1/2
Step 5 : repeat steps 3 and 4 for the next vertex
![]()
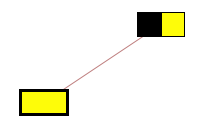
the probability of node assuming it' s chosen color is 1
Step 6: repeat steps 3 and 4 again
![]()

Again the probability of remaining node taking black is 1
Step 7: multiply together the marginal probabilities
![]()