Mathematica bits
Tips for Mathematica users
Monday, January 30, 2012
Mathematica Stack Exchange launched
After more than a year, the proposal for separate Mathematica stack exchange platform has been approved, and the site has been launched.
http://mathematica.stackexchange.com/
So far it seems quite active, and I was able to get my question answered within minutes.
Visualizing SDP cone
One way to visualize cone of positive semi-definite matrices is to take random 2D sections of the cone. Example is below, from images it's clear this region is non-smooth
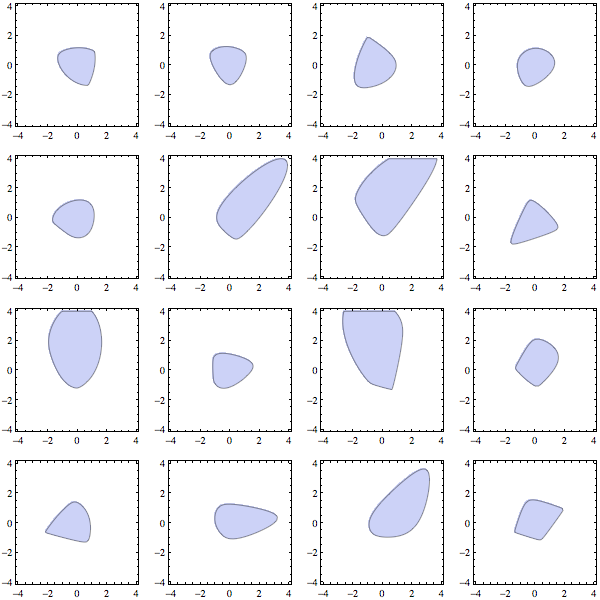
It doesn't look as instructive in 3D, but for example of doing the same in 3D, see this Mathematica stackexchange post
spectro13 := (
X = ( {
{x1, x2, x3, x7},
{x2, x4, x5, x8},
{x3, x5, x6, x9},
{x7, x8, x9, x10}
} );
vars = Union@Flatten@X;
dvars = {x, y};
m = Length@vars;
n = Length@dvars;
makeMat := X /. (Thread[vars -> #]) &;
proj = makeMat /@ Orthogonalize@RandomReal[{-1, 1}, {n, m}];
mat2 = Total@MapThread[Times, {proj, dvars}, 1] +
IdentityMatrix@Length@X;
cons = And @@ (Thread[Eigenvalues[mat2] >= 0]);
RegionPlot[cons, {x, -4, 4}, {y, -4, 4}, PlotPoints -> 15]
);
GraphicsGrid[Table[spectro13, {3}, {3}], ImageSize -> 600]

It doesn't look as instructive in 3D, but for example of doing the same in 3D, see this Mathematica stackexchange post
Tuesday, July 12, 2011
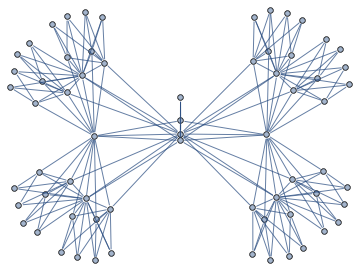
Visualizing language-script relationships
Graph below was obtained by processing language and script tags of about .5 billion web pages. Different character shapes were obtaining using custom VertexShapeFunction

Full image
Notebook

Full image
Notebook
Friday, March 25, 2011
Graph utilities I use
There's a number of graph utilities and tricks I use when working with graphs in Mathematica 8, I've summarized them in notebook graphUsage.nb. You can get this notebook and all required packages here.
Brief overview:
Fixing annoyances
programmatically changing style of existing graph, modifying graphs without forgetting vertex coordinates, using GraphPlot's layout for Graph objects, aligning adjacency matrix with vertex labels in index graphs
Listing graph structures
cliques, independent sets, maximal cliques, maximal independent sets, hamiltonian circuits
Visualizing graphs
Showing all graphs that miss particular properties, visualizing graphs with intensity attached to vertices -- pieGraph and fadedGraph. Showing graph with several types of vertices.
Brief overview:
Fixing annoyances
programmatically changing style of existing graph, modifying graphs without forgetting vertex coordinates, using GraphPlot's layout for Graph objects, aligning adjacency matrix with vertex labels in index graphs
Listing graph structures
cliques, independent sets, maximal cliques, maximal independent sets, hamiltonian circuits
Visualizing graphs
Showing all graphs that miss particular properties, visualizing graphs with intensity attached to vertices -- pieGraph and fadedGraph. Showing graph with several types of vertices.
Thursday, March 3, 2011
Computing Lovasz Theta function
One application of semi-definite programming is finding largest independent sets, or largest cliques in graph. According to Lovasz "Semidefinite programs and combinatorial optimization", SDP is the only known tractable way to find largest clique/independent set in perfect graphs.
One approach I've seen relies on the Lovasz theta function. Lovasz theta function is an estimate of independence number of the graph, and theta of graph's complement is guaranteed to lie between graphs's clique number and its chromatic number. Clique number and chromatic number are NP-complete, yet Lovasz theta function can be found in polynomial time using SDP. In perfect graphs and their complements, clique number and chromatic number coincide, which means that estimate from Lovasz theta function becomes exact.
I've put a function to compute Lovasz theta function using CVXOPT into package sdp2 below. You need to have CVXOPT and Pythonika installed as described here You could use it as follows
This gives $\sqrt{13}$
Package also has a function "minimizeSpectralRadius" which finds matrix of smallest spectral radius subject to element constraints, and "lovaszComplete" which creates a graph by thresholding solution of "minimum spectral radius" formulation of Lovasz theta function (p.26 of Lovasz). Curiously, lovaszComplete reaches fixed point after 1 iteration for all graphs I tried --
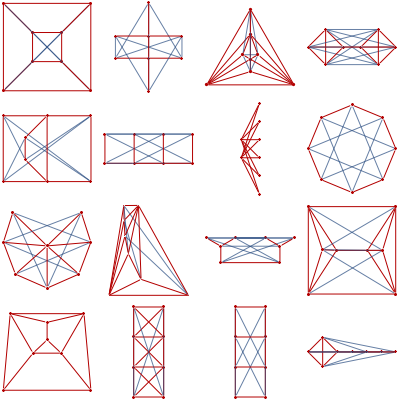
Red edges are original graph, blue are positive entries introduced when solving the SDP

SDP2 package
One approach I've seen relies on the Lovasz theta function. Lovasz theta function is an estimate of independence number of the graph, and theta of graph's complement is guaranteed to lie between graphs's clique number and its chromatic number. Clique number and chromatic number are NP-complete, yet Lovasz theta function can be found in polynomial time using SDP. In perfect graphs and their complements, clique number and chromatic number coincide, which means that estimate from Lovasz theta function becomes exact.
I've put a function to compute Lovasz theta function using CVXOPT into package sdp2 below. You need to have CVXOPT and Pythonika installed as described here You could use it as follows
Install["/Users/Yaroslav/mathematica/Pythonika"];
SetDirectory[NotebookDirectory[]];
Needs["Bulatov`sdp2`"];
theta = lovaszTheta@GraphData[{"Paley", 13}];
RootApproximant@theta
This gives $\sqrt{13}$
Package also has a function "minimizeSpectralRadius" which finds matrix of smallest spectral radius subject to element constraints, and "lovaszComplete" which creates a graph by thresholding solution of "minimum spectral radius" formulation of Lovasz theta function (p.26 of Lovasz). Curiously, lovaszComplete reaches fixed point after 1 iteration for all graphs I tried --

Red edges are original graph, blue are positive entries introduced when solving the SDP

SDP2 package
Semidefinite programming in Mathematica using CVXOPT
One can get access to semidefinite programming from Mathematica by using Pythonika to interface with Python's cvxopt package.
For MacOS 10.6 and Mathematica 8 the following should work
If your compilation doesn't work, post a follow-up comment here
Then you can use my package Bulatov`sdp1 to get direct access to one common form of SDP -- maximize a linear function of a matrix subject to positive-definiteness and element value constraints.
As an example application, consider MAXCUT -- find partition of the vertices such that number of edges connecting vertices from different partitions is maximized.
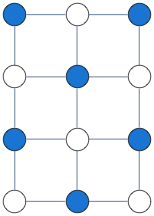
Solution above was obtained by solving a binary integer quadratic program, as follows
SDP relaxation gives a guaranteed approximation to binary quadratic program above --
This gives the same solution for the example above, but is much faster. solveDualSDP here finds psd matrix X that maximizes -A.X with diagonal entries of X constrained to be 1. For more details on this formulation, see Chapter 6 of Williamson,Shmoys, Design of Approximation Algorithms. For details of how to convert SDPs to standard vectorized form as used by CVXOPT, see this post

Packages
Notebook
For MacOS 10.6 and Mathematica 8 the following should work
- Install 64-bit Python 2.7 distribution from official site
- Get latest cvxopt sources and make
- Get Pythonika sources from google site
- copy mathlink.framework (in /Applications/Mathematica.app/SystemFiles/Links/MathLink/DeveloperKit/CompilerAdditions/) to /Library/Frameworks directory
- Fill correct paths in Pythonika Makefile, also add "-lstdc++ -framework CoreFoundation" linker flags
- In Pythonika Makefile, rename libML.a into libMLi3.a
If your compilation doesn't work, post a follow-up comment here
Then you can use my package Bulatov`sdp1 to get direct access to one common form of SDP -- maximize a linear function of a matrix subject to positive-definiteness and element value constraints.
As an example application, consider MAXCUT -- find partition of the vertices such that number of edges connecting vertices from different partitions is maximized.

Solution above was obtained by solving a binary integer quadratic program, as follows
g = GridGraph[{4, 3}];
A = AdjacencyMatrix@g;
n = Length@VertexList@g;
u = ConstantArray[1, n];
vars = x /@ Range@n;
cons = And @@ (-1 <= x[#] <= 1 & /@ Range@n);
solution=vars /. Last[Maximize[{-vars.A.vars, cons}, vars, Integers]]SDP relaxation gives a guaranteed approximation to binary quadratic program above --
Needs["Bulatov`sdp1`"];
Install["/Users/Yaroslav/mathematica/Pythonika"];
gram = solveDualSDP[-A, IdentityMatrix[n], u];
solution = gramRound[gram];
This gives the same solution for the example above, but is much faster. solveDualSDP here finds psd matrix X that maximizes -A.X with diagonal entries of X constrained to be 1. For more details on this formulation, see Chapter 6 of Williamson,Shmoys, Design of Approximation Algorithms. For details of how to convert SDPs to standard vectorized form as used by CVXOPT, see this post

Packages
Notebook
Friday, February 25, 2011
Plotting over 3d simplex
Someone on stackoverflow asked how to plot a function over 3d simplex.
I put together the code that takes care of rotations into "simplexPlot" and also used a recipe from math.SE for traditional 3D axes. Below is simplex plot of Sin[x y z]
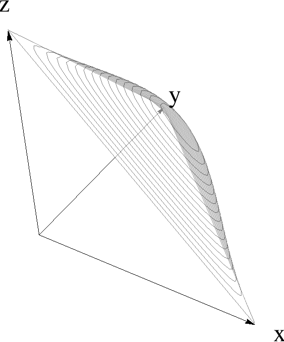
The function "simplexPlot" in notebook plots the function in x-y plane. Function "axes" does traditional 3d axes. To visualize the connection to the original simplex domain, I rotate the whole plot back into original domain
Notebook
I put together the code that takes care of rotations into "simplexPlot" and also used a recipe from math.SE for traditional 3D axes. Below is simplex plot of Sin[x y z]

The function "simplexPlot" in notebook plots the function in x-y plane. Function "axes" does traditional 3d axes. To visualize the connection to the original simplex domain, I rotate the whole plot back into original domain
t = AffineTransform[{{{-(1/Sqrt[2]), -(1/Sqrt[6]),
1/Sqrt[3]}, {1/Sqrt[2], -(1/Sqrt[6]), 1/Sqrt[3]}, {0, Sqrt[2/3],
1/Sqrt[3]}}, {1/3, 1/3, 1/3}}];
graphics = simplexPlot[5 Sin[#1 #2 #3] &, Plot3D];
shape = Cases[graphics, _GraphicsComplex];
gr = Graphics3D[{Opacity[.5], GeometricTransformation[shape, t]},
Axes -> False, Boxed -> False, Lighting -> "Neutral"];
Show[gr, axes[1, 1, 1, 0.05, 0.02]]Notebook
Thursday, February 24, 2011
Hyperpublic programming challenge
A start-up put up a small programming challenge.
There was some doubt whether the automatic answer key was correct, so I decided to check the answers using Mathematica. (note, it might be considered cheating to submit solutions obtained using Mathematica)
The first problem asks to find "influence" which comes down to the problem of counting descendants of each node in a graph, and can be done using recursion with memoization. Using Daniel Lichtblau's suggestion on how to parse the adjacency matrix, here's the whole solution.
Checking the answer to the second "hard" problem is actually easier than the first because you can use Mathematica's MIP solver. The problem basically asks for the smallest number of integers of several different type needed so that their sum adds up to a given total. Here's how you could do it in Mathematica
There was some doubt whether the automatic answer key was correct, so I decided to check the answers using Mathematica. (note, it might be considered cheating to submit solutions obtained using Mathematica)
The first problem asks to find "influence" which comes down to the problem of counting descendants of each node in a graph, and can be done using recursion with memoization. Using Daniel Lichtblau's suggestion on how to parse the adjacency matrix, here's the whole solution.
words = ReadList["challenge2input.txt", Word];
mat = Map[Characters, words] /. {"O" -> 0, "X" -> 1};
inf[i_] := (inf[i] =
1 + If[Total[mat[[i]]] == 0, 0,
Total[inf /@ Flatten@Position[mat[[i]], 1]]]);
influences = inf /@ Range@Length@mat - 1;
top3 = (Reverse@Sort@influences)[[;; 3]];
answer1 = StringJoin[ToString /@ top3]
Checking the answer to the second "hard" problem is actually easier than the first because you can use Mathematica's MIP solver. The problem basically asks for the smallest number of integers of several different type needed so that their sum adds up to a given total. Here's how you could do it in Mathematica
mintasks[total_] := (
types = {2, 3, 17, 23, 42, 98};
vars = x /@ Range@Length@types;
poscons = And @@ (# >= 0 & /@ vars);
First@Minimize[{Total[vars], vars.types == total && poscons}, vars,
Integers]
);
counts = mintasks /@ {2349, 2102, 2001, 1747};
answer2 = Times @@ counts
Wednesday, February 9, 2011
Chordal graph package update
I've fixed some bugs and added chordal-usage.nb (HTML) notebook with examples on how to do the following things with the chordal graph package:
- checking if the graph is chordal
- making graph chordal by adding fill edges using minimum fill heuristic
- getting perfect elimination ordering of a chordal graph
- arranging chordal matrix in perfect order
- arranging general sparse matrix in order that minimizes extra fill added by cholesky decomposition
- getting maximal cliques of a chordal graph
- getting clique tree structure of a chordal graph
- generating a chordal graph with given tree width and given tree structure
Description of methods is in Blair's excellent "An introduction to chordal graphs and clique trees" monograph

Chordal graphs release2
- checking if the graph is chordal
- making graph chordal by adding fill edges using minimum fill heuristic
- getting perfect elimination ordering of a chordal graph
- arranging chordal matrix in perfect order
- arranging general sparse matrix in order that minimizes extra fill added by cholesky decomposition
- getting maximal cliques of a chordal graph
- getting clique tree structure of a chordal graph
- generating a chordal graph with given tree width and given tree structure
Description of methods is in Blair's excellent "An introduction to chordal graphs and clique trees" monograph

Chordal graphs release2
Tuesday, February 8, 2011
Chordal graph utilities
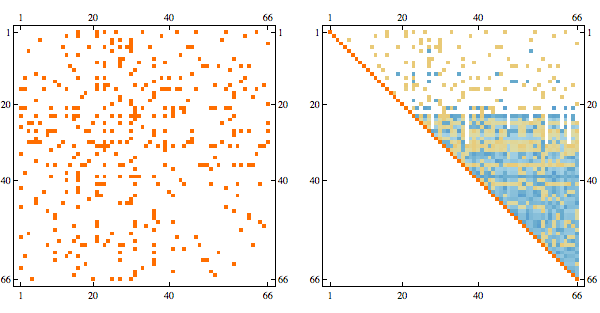
Here's visualization of a matrix and its Cholesky factorization
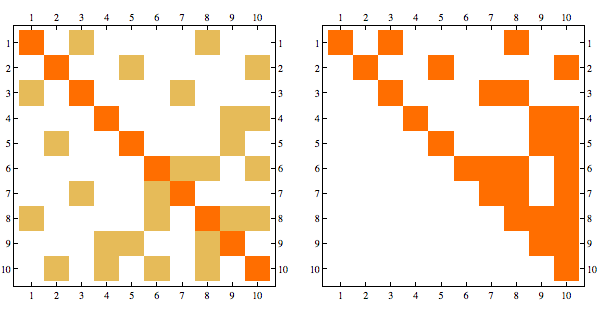
The sparsity pattern in the Cholesky factorization corresponds to the adjacency matrix of the graph triangulated using canonical ordering. This triangulation involves adding so called "fill" edges and can be visualized below
A matrix whose rows/columns can be symmetrically permuted to give Cholesky factorization with no extra fill cells is known as a "chordal" matrix, and a graph corresponding to that sparsity structure is known as chordal graph. Rearrangement of indices that produces factorization with no extra fill is known as "perfect elimination ordering".
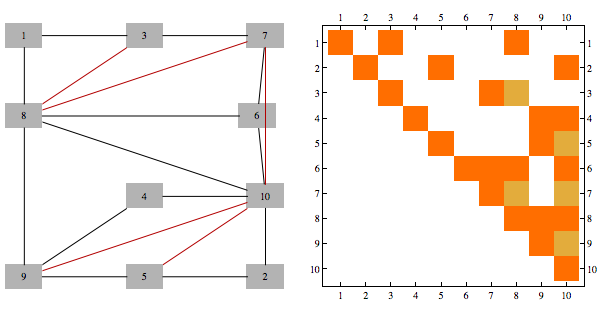
Consider the following matrix and its Cholesky decomposition
This matrix is chordal, and perfect elimination ordering corresponds to reversing the order of rows/columns, here's the Cholesky decomposition with order reversed
When the matrix is not chordal, perfect elimination ordering is not possible, but you could still try to rearrange the indices to make result of symmetric Gaussian elimination as sparse as possible, this is known as min fill ordering. Greedy min-fill search will find perfect elimination ordering if one exists.
To arrange symmetric matrix A to make its Cholesky factorization as sparse as possible using greedy min fill search, do the following
Here's an example of a structured sparse matrix and its Cholesky decomposition
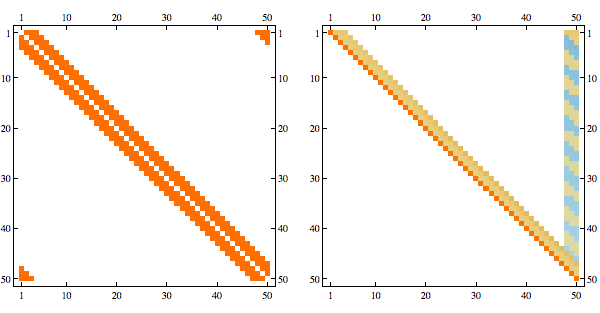
Here's the result after randomly permuting indices
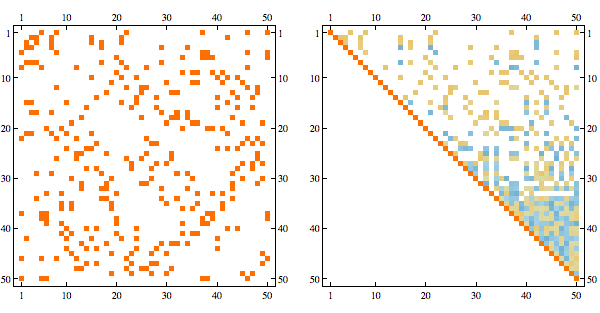
Using greedy minfill ordering we can recover some of the original structure
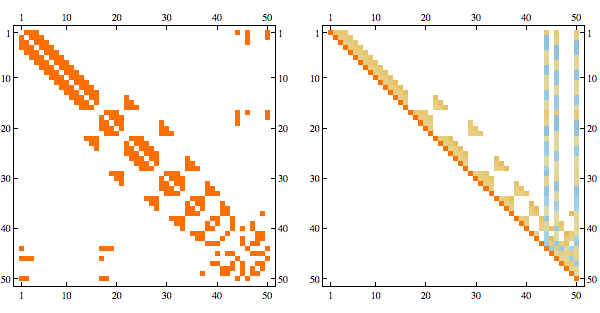
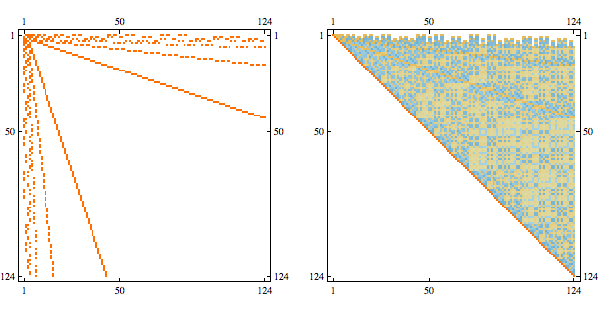
Here's a more complex example with non-linear structure
it's a matrix with sparsity pattern corresponding to the following graph
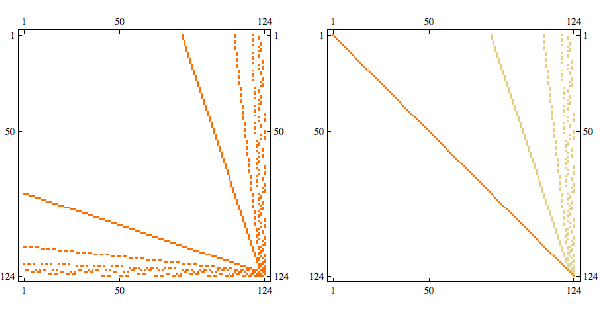
Randomly permuting indices we get the following
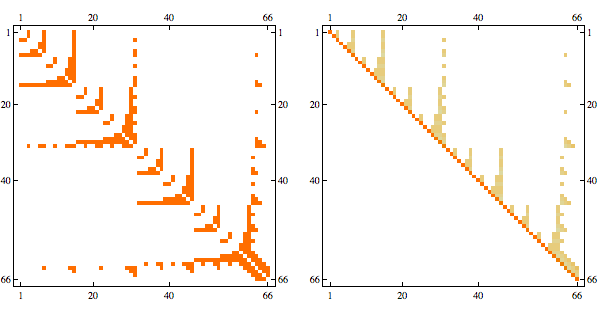
And here's the result in minfill order
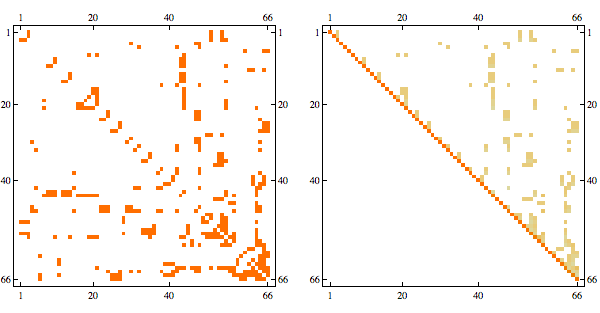

Notebook
Packages

The sparsity pattern in the Cholesky factorization corresponds to the adjacency matrix of the graph triangulated using canonical ordering. This triangulation involves adding so called "fill" edges and can be visualized below

A matrix whose rows/columns can be symmetrically permuted to give Cholesky factorization with no extra fill cells is known as a "chordal" matrix, and a graph corresponding to that sparsity structure is known as chordal graph. Rearrangement of indices that produces factorization with no extra fill is known as "perfect elimination ordering".
Consider the following matrix and its Cholesky decomposition

This matrix is chordal, and perfect elimination ordering corresponds to reversing the order of rows/columns, here's the Cholesky decomposition with order reversed

When the matrix is not chordal, perfect elimination ordering is not possible, but you could still try to rearrange the indices to make result of symmetric Gaussian elimination as sparse as possible, this is known as min fill ordering. Greedy min-fill search will find perfect elimination ordering if one exists.
To arrange symmetric matrix A to make its Cholesky factorization as sparse as possible using greedy min fill search, do the following
Needs{"Bulatov`chordal`"];
order = getMinFillOrder[AdjacencyGraph@Unitize@A];
CholeskyDecomposition[A[[Reverse@order, Reverse@order]]]Here's an example of a structured sparse matrix and its Cholesky decomposition

Here's the result after randomly permuting indices

Using greedy minfill ordering we can recover some of the original structure

Here's a more complex example with non-linear structure

it's a matrix with sparsity pattern corresponding to the following graph

Randomly permuting indices we get the following

And here's the result in minfill order


Notebook
Packages
Monday, February 7, 2011
Cluster variation method example
Cluster variation methods for search work by approximating the distribution over satisfying instances, and then using marginals of that distribution to guide the search.
For instance, when trying to find largest independent set, you would specify probability distribution where probability of independent set k is proportional to lambda^size(k). As lambda goes to infinity, probability mass gets concentrated on nodes that are contained in the largest independent set
Here's an animation of occupation probability marginals with lambda going from 0 to 3. You can see the mass gets concentrated on nodes that are part of the largest independent set in the graph, at which point you can use greedy search
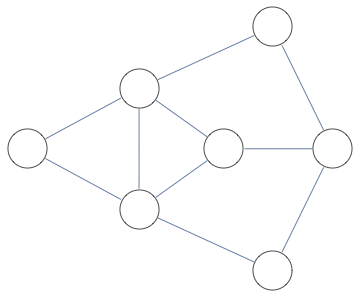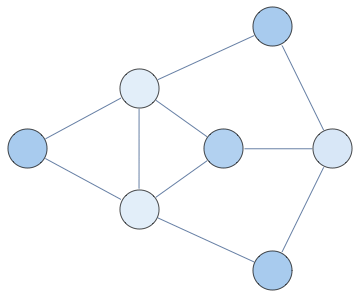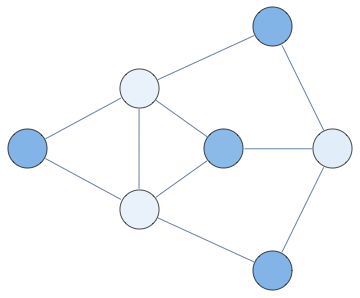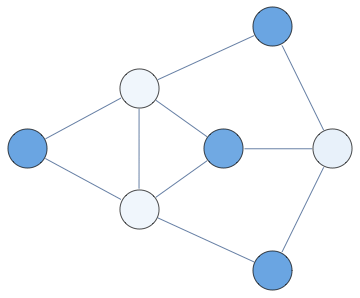
 Notebook+packages
Notebook+packages
For instance, when trying to find largest independent set, you would specify probability distribution where probability of independent set k is proportional to lambda^size(k). As lambda goes to infinity, probability mass gets concentrated on nodes that are contained in the largest independent set
Here's an animation of occupation probability marginals with lambda going from 0 to 3. You can see the mass gets concentrated on nodes that are part of the largest independent set in the graph, at which point you can use greedy search

 Notebook+packages
Notebook+packages
Wednesday, February 2, 2011
Making cross-words with Mathematica
A recent question on Stack Overflow asked how to use Mathematica to find a complete grid of words like this

Each row and each column must be a valid word.
A notebook below gives a way to solve this for small grids using SAT solver, and another answer in the post gives a pattern-based approach
 Notebook
Notebook

Each row and each column must be a valid word.
A notebook below gives a way to solve this for small grids using SAT solver, and another answer in the post gives a pattern-based approach
 Notebook
Notebook
Monday, January 31, 2011
Listing all Hamiltonian cycles of the graph
You can encode Hamiltonian cycle problem into SAT. It's more complicated than independent sets in previous post, but it can be done by assigning number to each vertex indicating its position in Hamiltonian cycle, constraining chosen edges to be consistent with vertex numbering, and using SatisfiabilityInstances to find all satisfying assignments
Here are the 12 cycles produced this way for BislitCube
Here are the constraints that were used
Smaller number of constraints can be used, but I found that increasing constraints makes SAT solver faster.
For these Graph Theory -> SAT encoding tasks, I find it helpful to have "formula"/ "vars" variables, and "decodeInstance"/"drawInstance" functions that so I can do something like this
decodeInstance turns variable assignment into readable/easy to process format, whereas drawInstance visualizes the instance as in pictures above.
Below is the notebook used to generate this diagram. It also has a helper .m file to draw a grid of all graphs with given set of properties. For instance, to show all graphs in GraphData that have 12 vertices, are Planar, Connected but are not Trees and fit in a 6x6 grid you would do

Name of graph shows up in Tooltip
 Notebook+package
Notebook+package
Here are the 12 cycles produced this way for BislitCube

Here are the constraints that were used
- Every vertex has one incoming and one outgoing edge
- Cycles of length 2 are forbidden
- Every vertex is assigned one number
- First vertex is assigned number 1
- Presence of edge i,j implies number of number(j)=number(i)+1 and the converse
Smaller number of constraints can be used, but I found that increasing constraints makes SAT solver faster.
For these Graph Theory -> SAT encoding tasks, I find it helpful to have "formula"/ "vars" variables, and "decodeInstance"/"drawInstance" functions that so I can do something like this
sats = SatisfiabilityInstances[formula, vars, 20];
drawInstance /@ sats
decodeInstance /@ sats
decodeInstance turns variable assignment into readable/easy to process format, whereas drawInstance visualizes the instance as in pictures above.
Below is the notebook used to generate this diagram. It also has a helper .m file to draw a grid of all graphs with given set of properties. For instance, to show all graphs in GraphData that have 12 vertices, are Planar, Connected but are not Trees and fit in a 6x6 grid you would do
Needs["Bulatov`showGraphs`"];
showGraphs[12, "Connected", ! "Tree", "Planar", gridSize -> 6]

Name of graph shows up in Tooltip
 Notebook+package
Notebook+package
Thursday, January 27, 2011
Using SAT solver to find independent sets
Here's a simple graph and all of its independent vertex sets
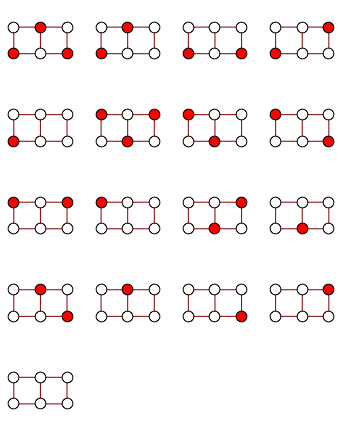
You can use SatisfiabilityInstances to get them as follows
Notebook

You can use SatisfiabilityInstances to get them as follows
gg = GridGraph[{2, 3}];
edge2clause[e_] := ! (e[[1]] && e[[2]]);
clauses = edge2clause /@ EdgeList[gg];
formula = And @@ clauses;
vars = VertexList[gg];
instances = SatisfiabilityInstances[formula, vars, 1000];
independentSets = Extract[vars, Position[#, True]] & /@ instancesNotebook
Monday, January 24, 2011
Counters in SAT
Here's a visualization of a SAT formula of a BooleanCountingFunction. Four circles in the middle are the variables of interest. Five circles on the periphery are variables encoding the number of true assignments of the four circles in the middle. Squares are clauses, and color of the edge indicates whether the variable is negated in that clause. You can see from the color that rightmost circle represents "all variables are true" and leftmost circle represents "all variables are false".
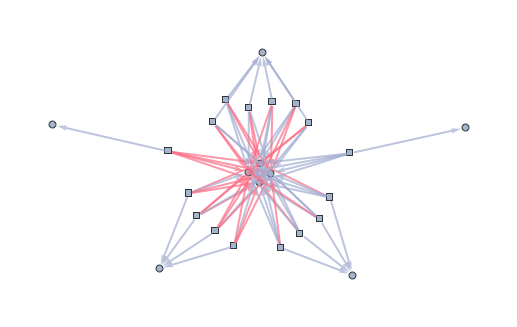
Notebook

Notebook
Friday, January 21, 2011
Tree decomposition package
A tree decomposition is a representation of a complete set of vertex separators of a graph. For instance, here's an Apollonian Network and its tree decomposition.
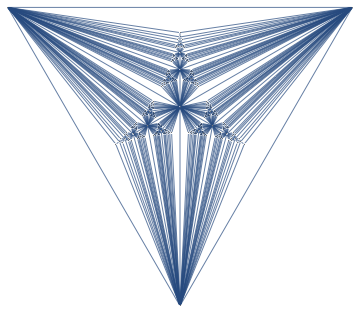
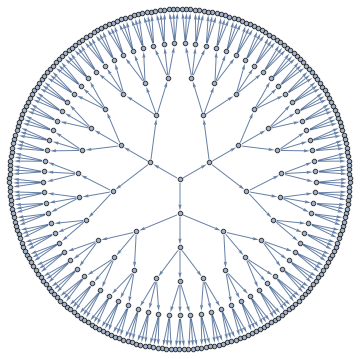
Decomposition above shows off 121 vertex separators of size 4, represented as non-leaf nodes, each separating graph into 3 parts, and 363 vertex separators of size 3, represented as edges, each separating the graph into 2 parts.
I put the tree decomposition code in a package. Unzip the file into any folder, and execute cells in treeDecomposition-usage.nb for the decomposition above. It takes 2 minutes for 367 vertex Apollonian network above. Graphs with around hundred vertices should take a few seconds.
Generally, to do a visualization like above, you'd do the following
Tree decomposition package


Decomposition above shows off 121 vertex separators of size 4, represented as non-leaf nodes, each separating graph into 3 parts, and 363 vertex separators of size 3, represented as edges, each separating the graph into 2 parts.
I put the tree decomposition code in a package. Unzip the file into any folder, and execute cells in treeDecomposition-usage.nb for the decomposition above. It takes 2 minutes for 367 vertex Apollonian network above. Graphs with around hundred vertices should take a few seconds.
Generally, to do a visualization like above, you'd do the following
<< Bulatov`treeDecomposition`;
g = GraphData[{"Apollonian", 5}];
{nodes, edges} = findTreeDecomposition[g];
GraphPlot[Rule @@@ edges]
Tree decomposition package
Saturday, January 15, 2011
Coloring overlapping circles
Take some overlapping circles
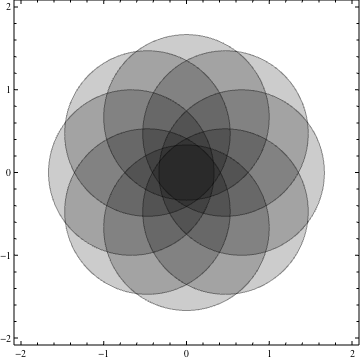
What if we want to color overlapping regions according to how many overlaps they had?
We can use "BooleanCountingFunction" as follows
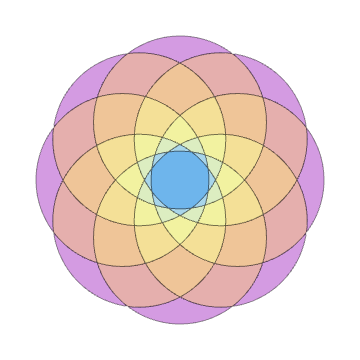
nc = 8;
ineqs = Table[(x - 2/3 Cos[i 2 Pi/nc])^2 + (y -
2/3 Sin[i 2 Pi/nc])^2 < 1, {i, 0, nc - 1}];
Show[Table[
RegionPlot[ineqs[[k]], {x, -2, 2}, {y, -2, 2}, PlotPoints -> 35,
PlotStyle -> Opacity[.2]], {k, 1, nc}]]

What if we want to color overlapping regions according to how many overlaps they had?
We can use "BooleanCountingFunction" as follows
plots = Table[
RegionPlot[
BooleanCountingFunction[{k}, ineqs], {x, -2, 2}, {y, -2, 2},
PlotPoints -> 100, Frame -> None,
PlotStyle -> ColorData["Pastel"][k/nc]], {k, 0, nc}];
GraphicsGrid@Partition[plots, 3]
Show[Rest[plots]]


Saturday, January 8, 2011
Independence Polynomials with Tree Decomposition
A lot of NP-hard problems on graphs become easy if you find a good tree decomposition of the graph.
Essentially, tree decomposition asks for a way to take a set of small sets of vertices and connect them in a way so that vertices shared by any pair of connected sets is a separator of the graph.
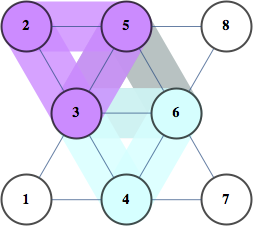
Two examples below show a graph on the left and it's optimal tree decomposition on the right
Following problems become easy once you have a good tree decomposition of a graph. Finding best: clique, independent set, dominating set, TSP tour, Steiner Tree. Almost every graph polynomial is tractable to compute given good tree decomposition. Finding BEST tree decomposition is NP-hard, but finding good decomposition is much easier. It parallelizes well, and simple heuristics give decompositions close to optimal for moderate size graphs even on my two-processor laptop.
Here are two relevant notebooks:
Essentially, tree decomposition asks for a way to take a set of small sets of vertices and connect them in a way so that vertices shared by any pair of connected sets is a separator of the graph.
Two examples below show a graph on the left and it's optimal tree decomposition on the right
 | 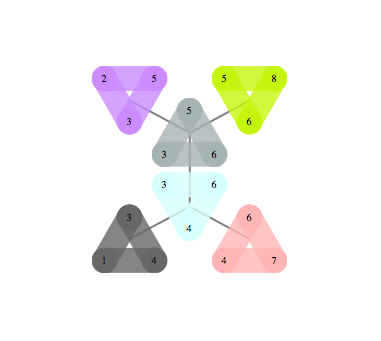 |
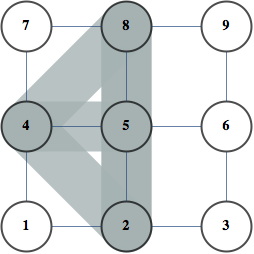 | 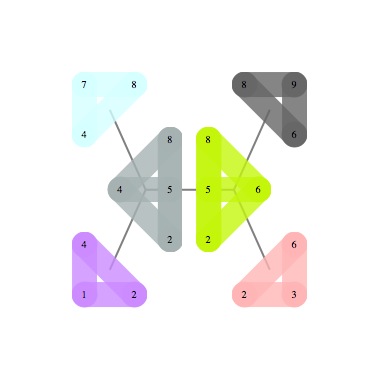 |
Following problems become easy once you have a good tree decomposition of a graph. Finding best: clique, independent set, dominating set, TSP tour, Steiner Tree. Almost every graph polynomial is tractable to compute given good tree decomposition. Finding BEST tree decomposition is NP-hard, but finding good decomposition is much easier. It parallelizes well, and simple heuristics give decompositions close to optimal for moderate size graphs even on my two-processor laptop.
Here are two relevant notebooks:
Friday, January 7, 2011
Making Error Correcting code with FindIndependentVertexSet
Suppose you want to transmit information over a lossy channel. Your channel flips some bits at random and you want to choose your code-words so that you can recover the original codeword with high probability.
One approach is to pick a set of codewords of length n so that the Hamming distance between any two of them is at least d. This means that if the number of errors is less than (d-1)/2, you can recover the original word by picking code word closest in Hamming distance to the received word.
For example, for 3 bits and d=2, the code would be
Essentially when d=2, this is equivalent to finding a set of non-adjacent vertices of hypercube in n dimensions. For instance, code above can be visually represented as follows

For n=4 we can visualize it as follows

Essentially the problem is one of independent set, we construct a graph where vertices correspond to codewords and are connected if and only if hamming distance between them is 1.
Two graphs above correspond to "CubicalGraph" and "TesseractGraph" in GraphData, but if you want to recover the codewords, you want to control the ordering of vertices and construct the graph yourself. Getting the code is straightforward from the independent vertex set
The result gives you a set of code-words over n-bits that are at least 2 bit flips apart from one another.
Now suppose we want to make our code more robust against errors. We construct graph as before, but augment it with the command "GraphPower[g,d-1]" to create a graph where vertices in an independent set are at least d steps apart. For n=6,d=2, VertexIndependentSet finds a code consisting of 8 codewords, which is the best possible.
It is known that for n=7,d=3 there's a code consisting of 16 codewords, although this problem seems to be too difficult to solve using version of VertexIndependentSet that ships with version 8.0
I'm experimenting with a message passing algorithm to solve this problem in the independent vertex set formulation, I'll post an update if it turns out better than the built-in
 Notebook
Notebook
One approach is to pick a set of codewords of length n so that the Hamming distance between any two of them is at least d. This means that if the number of errors is less than (d-1)/2, you can recover the original word by picking code word closest in Hamming distance to the received word.
For example, for 3 bits and d=2, the code would be
100
010
001
111
Essentially when d=2, this is equivalent to finding a set of non-adjacent vertices of hypercube in n dimensions. For instance, code above can be visually represented as follows

For n=4 we can visualize it as follows

Essentially the problem is one of independent set, we construct a graph where vertices correspond to codewords and are connected if and only if hamming distance between them is 1.
Two graphs above correspond to "CubicalGraph" and "TesseractGraph" in GraphData, but if you want to recover the codewords, you want to control the ordering of vertices and construct the graph yourself. Getting the code is straightforward from the independent vertex set
words = Tuples[{0, 1}, 4];
distMat = Outer[HammingDistance, words, words, 1];
g = AdjacencyGraph[Map[Boole[# == 1] &, distMat, {2}]];
verts = FindIndependentVertexSet[g];
code = words[[verts]]The result gives you a set of code-words over n-bits that are at least 2 bit flips apart from one another.
Now suppose we want to make our code more robust against errors. We construct graph as before, but augment it with the command "GraphPower[g,d-1]" to create a graph where vertices in an independent set are at least d steps apart. For n=6,d=2, VertexIndependentSet finds a code consisting of 8 codewords, which is the best possible.
It is known that for n=7,d=3 there's a code consisting of 16 codewords, although this problem seems to be too difficult to solve using version of VertexIndependentSet that ships with version 8.0
I'm experimenting with a message passing algorithm to solve this problem in the independent vertex set formulation, I'll post an update if it turns out better than the built-in
 Notebook
Notebook
Sunday, January 2, 2011
Magic Square
Here's an interesting tidbit I saw linked from reddit -- the following decimal expansions form a magic square

Here's how you'd check the row and column sums

Here's how you'd check the row and column sums
v = 18;
row[k_] := PadLeft[IntegerDigits[Floor[k/(v + 1)*10^v]], v];
mat = row /@ Range[v];
Total@mat
Total@Transpose@mat
Saturday, January 1, 2011
Making web animations
I came across this cool animation on Sander Huisman's blog. Original animation was a lossy YouTube link, and it doesn't do it justice. The way to get a high-quality embedded animation is to generate individual frames and then export to Flash format as follows
Export["~/research/qr/hinges/anim.swf", images];
Then include the following snippet in your page. Location of the swf file goes in two places, allegedly to provide compatibility for IE+Mozilla browsers
Notebook
Friday, December 31, 2010
Making anti-aliased diagrams
Even though Mathematica supports anti-aliasing for 3D graphics, it's done inside the video-card which often make computational shortcuts and anti-aliasing quality is sub-optimal. A better way is to rasterize your diagram at higher resolution before exporting, as follows
is=360;
raster=Rasterize[graphic, ImageSize -> is, RasterSize -> 2 is];
Export["~/image.png",raster];
Notebook
Thursday, December 30, 2010
How to get Mathematica help
Online sources:
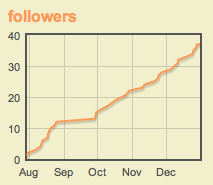
Eventually there may be a separate stack exchange for Mathematica users. The proposal is here and the number of followers has been steadily going up.
It helps to include self-contained piece of code in your question illustrating the issue.
Two guidelines:
- stack overflow: post your question and make sure to include "mathematica" in tags. This is the fastest way and usually you get an answer within 30 minutes. A couple of WRI employees occasionally answer questions there.
- Mathematica newsgroup: if you are willing to wait a day for the answer, it can be helpful. Questions containing explicit mentions of competing systems will be rejected, so if you have a question along the lines of "I need to implement an equivalent of OrbitsDomain in GAP", you need to say "I need a function that works similar to OrbitsDomain in a certain open-source group theory package". I usually turn to newsgroup when the stackoverflow community can not answer, and have occasionally gotten very insightful responses.
- Math stack exchange: use it when your question has significant math component and use "mathematica" tag. Answer will possibly tell you how to do this in some other system
Eventually there may be a separate stack exchange for Mathematica users. The proposal is here and the number of followers has been steadily going up.

It helps to include self-contained piece of code in your question illustrating the issue.
Two guidelines:
- Make sure your code works on fresh kernel
- Search the forum for your question before asking it
Tuesday, December 21, 2010
Visualizing 7 dimensional simplex
One way to visualize a 7 dimensional simplex is to plot sections of it. You could restrict attention to (hyper)plane sections that go through points defined by averaging some set of vertices, and discard geometrically identical ones. There are only two such sections for 3d simplex
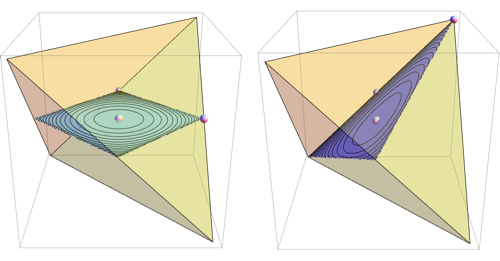
For 7d simplex, there are 49 such sections, and the most symmetrical one is the octahedron, which in the notebook below was found as the set of all 8 dimensional unit vectors with non-negative components orthogonal to (0, 3, 1, 0, -5, 0, 0, 1)

Here are all 49 distinct sections

Complete code is here.
An outline of how they were generated:
Notebook

For 7d simplex, there are 49 such sections, and the most symmetrical one is the octahedron, which in the notebook below was found as the set of all 8 dimensional unit vectors with non-negative components orthogonal to (0, 3, 1, 0, -5, 0, 0, 1)

Here are all 49 distinct sections

Complete code is here.
An outline of how they were generated:
- Use Peter Shor's observation that there's a homomorphism between distinct sections and ways to assign 8 identical objects to vertices of the cube
- Find such permutations by breaking space of all permutations of 8 objects into orbits under action of group of cube rotations and taking one representative from each orbit, using PermutationGroup, GroupElements and Permute, implemented as nonEquivalentPermutations
- Use BooleanCounting function and SatisfiabilityInstances to find assignment of vertices to centroids consistent with given cube representation, implemented as findAssignment
- Use NullSpace, Reduce and FindInstances to find 0-dimensional intersections of hyperplane defining the section with some subset of 8 simplex cells, implemented as getExtremePoints and getCons
- Those point sets define vertices of the section, use SingularValueDecomposition to find vertex sets with distinct sets of four non-zero singular values, implemented as singularCert and distinctPoses
- Project distinct point sets onto hyperplane defining the section and use ComputationalGeometry`Methods`ConvexHull3D to get description of the shape in terms of polygons, implemented as getVerts3D and getPoly
Notebook
Monday, December 20, 2010
Group theory bits
Suppose we want to get the number of ways of assigning 4 zeros and 4 ones to vertices of the cube, distinct under rotations of the cube. We can use similar approach as in the previous post, and while the relevant group of symmetry is not built into Mathematica, we can construct it manually from generators. Consider two rotations of the cube, one around vertical axis and another around horizontal
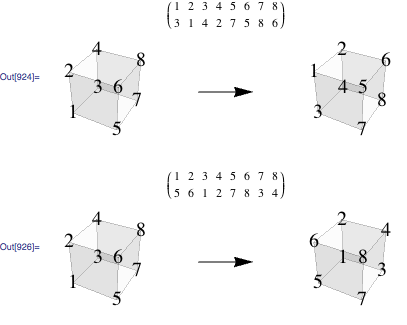
You can specify this group using generators above as permutation lists follows
Note, that there's more than one way to specify group using generators and they produce non-isomorphic Cayley graphs. Here are two more representations of the group above
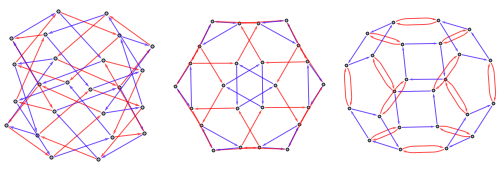
group2 uses rotation around axis through center of two faces and another rotation around long diagonal. This group is known to be isomorphic to the SymmetricGroup[4], so group3 uses standard generators of that group.
The last two graphs are planar so you plot them in 3D as polyhedra
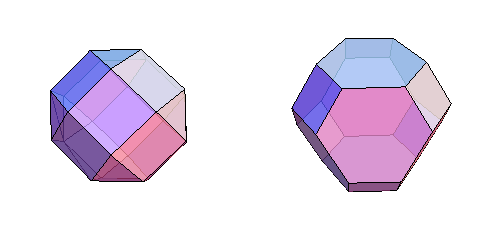
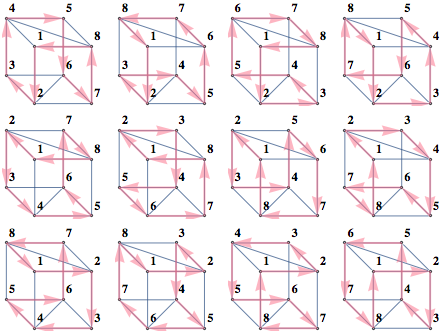
To generate all permutations of {1,1,1,1,0,0,0,0}, you could take a list of all permutations and weed out permutations identical under action of group1 or group2, using method from previous post. Even though group3 is isomorphic to our group, it's not represented as a subgroup of SymmetricGroup[8], so to use that method, we'd need to identify it as a subgroup of Symmetric Group[8]. We can do that by finding that a pi and 2pi/3 rotations of cube into itself. One axis is the long diagonal, and another goes through center of cube and centers of two cube edges, which gives the following representation
Here are the resulting 7 permutations
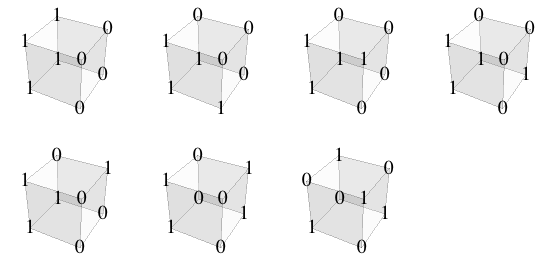
Notebook

You can specify this group using generators above as permutation lists follows
group1=PermutationGroup[PermutationCycles /@ {{3, 1, 4, 2, 7, 5, 8, 6},{5, 6, 1, 2, 7, 8, 3, 4}}];
Note, that there's more than one way to specify group using generators and they produce non-isomorphic Cayley graphs. Here are two more representations of the group above

group2 = PermutationGroup[
PermutationCycles /@ {{3, 1, 4, 2, 7, 5, 8, 6}, {7, 5, 3, 1, 8, 6,
4, 2}}];
group3 = SymmetricGroup[4];
CayleyGraph /@ {group1, group2, group3} //
GraphicsRow
group2 uses rotation around axis through center of two faces and another rotation around long diagonal. This group is known to be isomorphic to the SymmetricGroup[4], so group3 uses standard generators of that group.
The last two graphs are planar so you plot them in 3D as polyhedra

To generate all permutations of {1,1,1,1,0,0,0,0}, you could take a list of all permutations and weed out permutations identical under action of group1 or group2, using method from previous post. Even though group3 is isomorphic to our group, it's not represented as a subgroup of SymmetricGroup[8], so to use that method, we'd need to identify it as a subgroup of Symmetric Group[8]. We can do that by finding that a pi and 2pi/3 rotations of cube into itself. One axis is the long diagonal, and another goes through center of cube and centers of two cube edges, which gives the following representation
PermutationGroup[Cycles /@ {{{1, 2, 4, 3}, {5, 6, 8, 7}}, {{6, 3}, {5, 4}, {1, 2}, {7,8}}}]
Here are the resulting 7 permutations

Notebook
Subscribe to:
Posts (Atom)